stability of concrete structures under seismic loading
I completed my Ph.D. thesis at the Laboratoire de Mécanique et Technologie de l’ENS Paris-Saclay (formerly ENS Cachan), from 2012 to 2015, largely helped by the support of our horrendously big group of PhD students, and the always running coffee machine.
the science
Safety first! Thus, the structural integrity of nuclear power plants is deemed important. From that interesting observation, knowing in advance how containment walls in nuclear power plants react to an earthquake popping up nearby is essential. With a hint of abstraction, this problem can be rephrased as trying to develop accurate simulations of massive reinforced concrete structures facing cyclic loading paths. One of the key piece of information these simulations need to provide is how cracks form in concrete structures, and more precisely how much. Indeed, leaks in nuclear power plants containment walls are rarely a good thing…
The standard method to model such large structures is to consider the whole as a continuum, and therefore apply continuum mechanics. Equilibrium equations are solved using the finite element method, and the behaviour of the material is described using as precise and stable constitutive equations as possible. A key feature of these constitutive equations is their ability to reproduce the amount of dissipated energy partly due to fracture and partly due to mechanisms associated to oscillatory loadings.
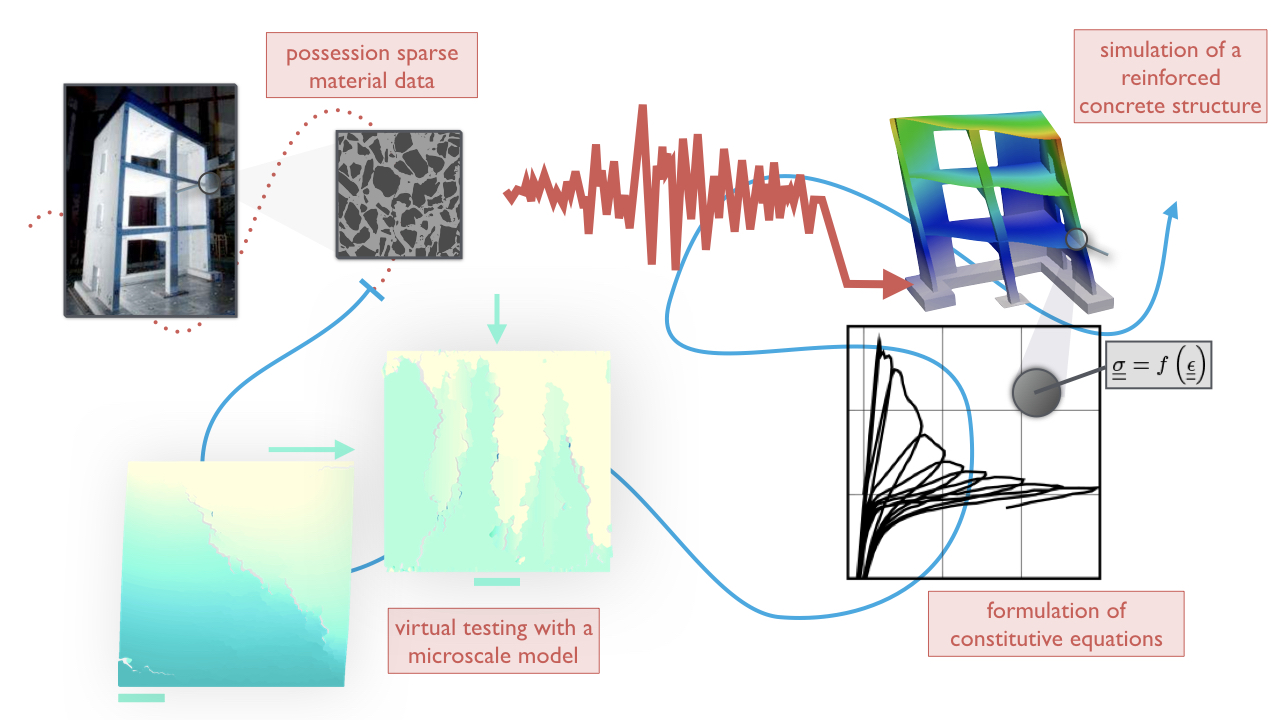highway to the prediction of the stability: methodology to predict from rare experimental data the stability of high-risk reinforced concrete structures such as containment buildings in nuclear power-plants facing earthquakes.
My research focused on studying and modelling concrete at two-scales: the scale of a batch of concrete and the scale of an engineering structural element. I tried to understand and model the mechanical behaviour of concrete under cyclic loading. Closure of cracks during unloading and reverse loading, causes a gradual regain of stiffness, but more surprisingly hysteresis.
Using a microscopic scale model for concrete, assuming homogeneity of the constituents but explicit description of cracking and partial representativity of cracks roughness, we explored failure under compressive loading [1] and later, phenomena arising under cyclic loadings. Monitoring contact and friction in formed cracks in a few centimetres large piece of concrete, we were able to understand how internal self-balanced pre-strains, released at cracking, can generate gradual stiffness recovery and hysteresis during unloading [2].
a not-so-simple shear test: simulation of a cracked concrete sample facing shear, showing significant crack surfaces interaction.
the devs
On the development side of things, which is what I did most during PhD project, I spent my time developing a microscale model of a batch of concrete. Originally it was an existing lattice model that I extended to a particle-based model, or as we call it now a beam-particle model [3]. In short, the continuum is discretised using Voronoï tessellation, polygonal particles are initially linked by brittle beams, and upon their failure can interact further by contact and friction. To enhance numerical stability, which was severely impaired by the simultaneous integration of brittle failure, contact and friction, I also redesigned the solution algorithm to solve quasi-static equilibrium [4].
Findings on the microscale mechanisms related to cracks closure led us to the formulation of a constitutive model for quasi-brittle materials cyclically loaded with enhanced numerical stability [2]. The model (source, example, notice) is now implemented and available in the open-source structural analysis and fluid mechanics software Cast3M based on the finite element method developed at the CEA.
the publications
[1] Maxime Vassaux, Benjamin Richard, Frédéric Ragueneau, and Alain Millard.
Compressive behavior of a lattice discrete element model for quasi-brittle materials.
Computational Modelling of Concrete Structures, 1 (2014): 335-344.
[2] Maxime Vassaux, Benjamin Richard, Frédéric Ragueneau, and Alain Millard.
Regularised crack behaviour effects on continuum modelling of quasi-brittle materials under cyclic loading.
Engineering Fracture Mechanics, 149 (2015): 18-36.
[3] Maxime Vassaux, Cécile Oliver-Leblond, Benjamin Richard, and Frédéric Ragueneau.
Beam-particle approach to model cracking and energy dissipation in concrete: Identification strategy and validation.
Cement and Concrete Composites, 70 (2016): 1-14.
[4] Maxime Vassaux, Benjamin Richard, Frédéric Ragueneau, Alain Millard, and Arnaud Delaplace.
Lattice models applied to cyclic behavior description of quasi‐brittle materials: advantages of implicit integration.
International Journal for Numerical and Analytical Methods in Geomechanics, 39 (2015): 775-798.