hierarchical toughening of polymer nanocomposites
Shortly before my funding was running out in Marseille, I started to have a decent idea of what I wanted like to explore on the long-run: relations between the cell mechanical environment and epigenetics. That is a very long shot, especially using computational models. Nevertheless, mentioning this at a few conferences, nobody said it was entirely stupid, so I started to believe… maybe… However, I was far from mastering the techniques to model anything below the scale of the cell nucleus. Long story short, got lucky, I found a position in London at the Centre for Computational Science at University College London, where I had to develop a tool to couple a method I knew, the Finite Element Method, and a method I needed to learn to model atomic systems, All-Atom Molecular Dynamics, being useful and learning at the same time!
the science
What if we could predict the material properties (Young modulus, thermal conductivity, and so on…) of a chemical compound for its atomic structure? To predict these properties computationally, we would need to simulate volumes of material of the order of the cubic centimetre, at the smallest, with details of the order of the nanometre, at the largest. Hopefully, there are a few simplifications we can perform, all the structural details from one end to the other need not to be considered, all the time, everywhere.
Polymer and derived nanocomposites are hierarchically structured materials, their structure evolves across the scales. Certain, characteristic scales, influence most significantly the behaviour of the nanocomposite. The structure of the material at these characteristic scales need to be considered in our models. At other scales, the information can, at first, be neglected. In short that is the philosophy of the methods developed at the Centre for Computational Science even before the start of this project [1].
Once we understand how the structure at each of these scales control the physics of the material, these structures can also be customised. Choosing a specific polymer, or adding tailor-made particles, for example, the properties of the resulting material can be enhanced with an engineering application in mind.
We modelled and coupled two characteristic scales: (i) the atomic structure using molecular dynamics, and (ii) the testing structure using the finite element method [2]. We were able to investigate how the addition of 2d-nanoparticles impact the response of thermosetting polymer to standard engineering tests, such as the dogbone tension test, the compact tension test or the drop-weight impact test. While applying loading conditions representative of the engineering continuum scale, our models enable to observe how the different constituents of the material interact at the atomic scale.



let’s give it a shot: simulation of a high-velocity impact on a composite shell made of pure epoxy cells and graphene-epoxy nanocomposite cells (top, left); the impact produces propagating compression and shear waves in the shell (top, right); the atomic structure of the nanocomposite located found at the centre of the shell faces high-frequency oscillations of mixed strains (bottom).
We mainly focused on fracture properties of the nanocomposites as it is a critical parameter in aeronautical design. We applied our multiscale modelling method to study how the material’s strength and toughness can be impacted by 2d-nanoparticles characteristics, for example their size, their thickness or their volume ratio. In the mean time we explored how thermosetting polymers such as epoxy resins, seemingly ductile at the nanoscale can become brittle at the macroscale. Quite unexpectedly, we first came to conclude that adding graphene nanoparticles in epoxy resins reduces drastically dissipated energy via internal friction during an impact test (see figure above). In other words, the nanoparticles enhance the elastic behaviour, energy restitution, of the thermosetting polymer [3]. These conclusions might not be extremely useful for airplane design, as impact rather need to be absorbed… but plenty of applications in sports performance, synthetic tissue engineering or energy-saving prosthetics could definitely benefit from these!
the devs
Methods and softwares available to simulate atomic and continuum systems are already plenty. At the nanoscale we developed an all-atom model of epoxy resin and epoxy resin traversed by a graphene sheet using LAMMPS, a molecular dynamics package. And, at the microscale we developed continuum two-phase model which equations were solved using Deal.II, a finite element method library. I initiated the development a coupling library, which name I didn’t think to much about, called DeaLAMMPS. The resulting software based on the heterogeneous mutliscale method allows to simulate a atomic and a continuum model concurrently [2]. The coupling is achieved by transfer of homogenised strains from the continuum to the atomic system and stresses the other way around. The two models exchanging mechanical information are, in result, loosely coupled and made it possible to understand how the interplay between the two given scales.
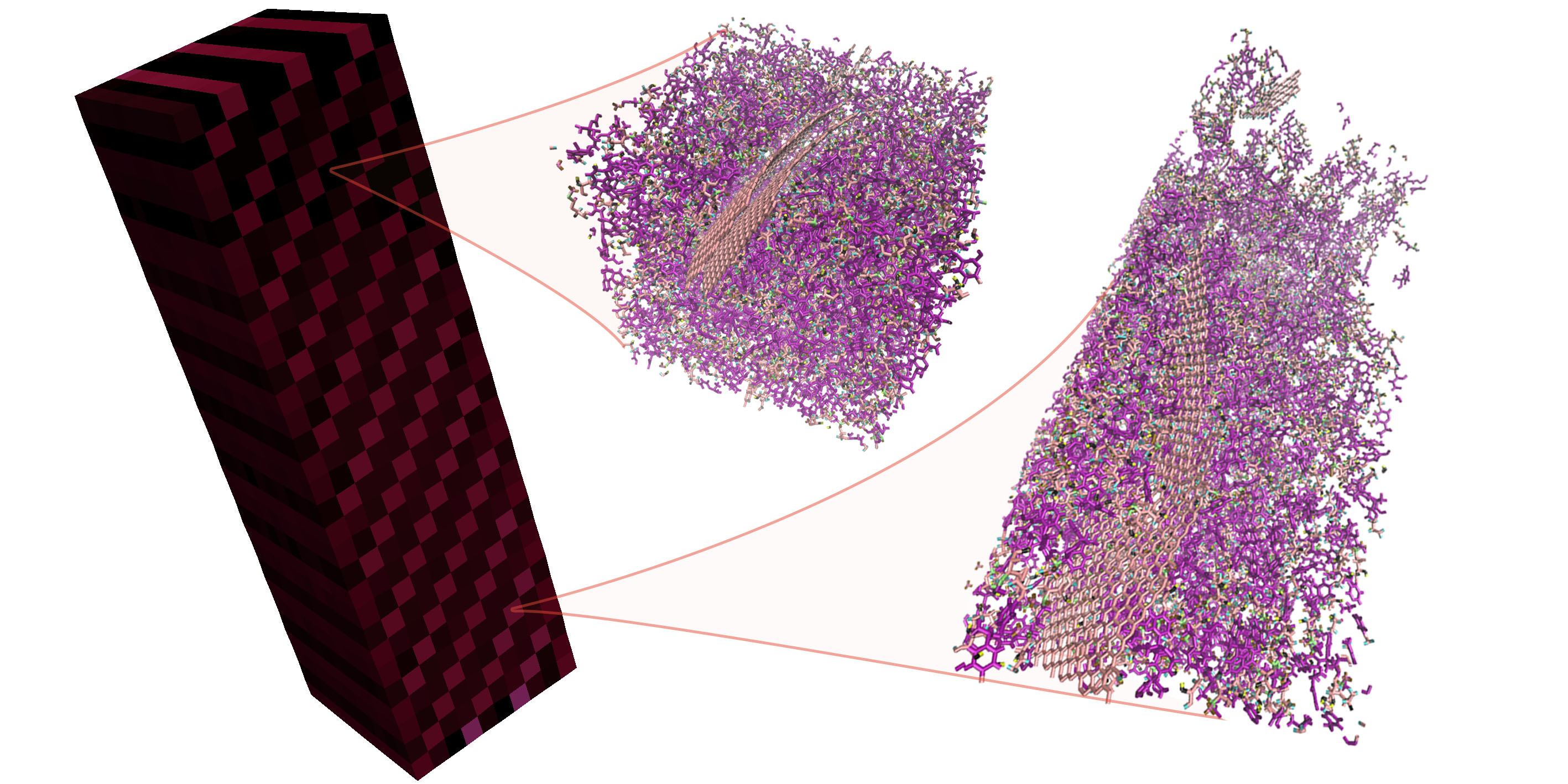
complex on so many levels: stress localisation in a continuum piece of graphene epoxy composite; the continuum scale model probes on two types of atomic systems involving single or double graphene reinforcement; the two types of composites are arranged in a diagonal pattern in the continuum.
An average two-scale simulation runs requires a few hundreds of thousands of core hours, simply put, quite a lot of computational energy… Thanks to allocations on supercomputers across Europe (ARCHER/UK, SuperMUC/Germany, PROMETHEUS/Poland), and a lot of optimisation in CPU usage, such highly parallel simulations were completed in a couple of days. Optimising multiscale parallel workflows was part of the European project ComPat. The project aimed at identifying patterns in computational workflows and automate the optimisation of their execution on several, distant resources, such as supercomputers. We took part in the optimisation of the execution of the computational patterns, where a “master” algorithm relies on operations performed by several instantiations of a “slave” algorithm, launched dynamically, asynchronously.
Running loads of multiscale simulations, coordinating large amounts of computations, might already be an achievement, however it is not considered sufficient to simply predict a result, that is property or mechanism. For any prediction to be trusted and worth acting upon, we better have an idea of its accuracy. Similarly to what experimentalists do, at least what I hope they do, tests need to be repeated to quantify confidence in the results. Uncertainty in simulations arises from many sources that can be grouped in three types: input parameter errors, verification errors (computer precision, mathematical accuracy), validation error (physical accuracy, range of validity). Quantifying uncertainty of multiscale simulations is the purpose of the European project VECMA, which led to the development of the VECMA toolkit [4]. The toolkit provides a suite of algorithms drawing from the specific structure of multiscale workflows to avoid the unbearable cost of Monte-Carlo methods to quantify uncertainty.
the publications
[1] Maxime Vassaux, Robert C. Sinclair, Robin A. Richardson, James L. Suter and Peter V. Coveney.
Toward high fidelity materials property prediction from multiscale modeling and simulation.
Advanced Theory and Simulations, In press (2019).
[2] Maxime Vassaux, Robin A. Richardson and Peter V. Coveney.
The heterogeneous multiscale method applied to inelastic polymer mechanics.
Philosophical Transactions of the Royal Society A, 377, 2142 (2019).
[3] Maxime Vassaux, Robert C. Sinclair, Robin A. Richardson, James L. Suter and Peter V. Coveney.
The role of graphene in enhancing the material properties of thermosetting polymers.
Advanced Theory and Simulations, 2, 5 (2019).
[4] Derek Groen, Robin A. Richardson, David W. Wright, Vytautas Jancauskas, Robert C. Sinclair, Paul Karlshoefer, Maxime Vassaux, Hamid Arabnejad, Tomasz Piontek, Piotr Kopta, Bartosz Bosak, Jalal Lakhlili, Olivier Hoenen, Diana Suleimenova, Wouter Edeling, Daan Crommelin, Anna Nikishova and Peter V. Coveney.
Introducing VECMAtk – verification, validation and uncertainty quantification for multiscale and HPC simulations.
In: Rodrigues J. et al. (eds) Computational Science – ICCS. Lecture Notes in Computer Science, vol 11539. Springer, Cham (2019).
